تقارن چیست

با هندسی اصطلاح تقارن ( یونان باستان συμμετρία symmetria Ebenmas، اندازه مساوی ، از σύν syn “together” و μέτρον metron ، اندازه گیری) ویژگی را توصیف می کند که یک شی هندسی از طریق حرکات بر روی خود نگاشت می تواند شود، یعنی بدون تغییر ظاهر شود. ریخته گری که یک شی را به خود نگاشت می کند، نگاشت تقارن یا عملیات تقارن نامیده می شود .

گاهی اوقات گفته می شود که دو (یا چند) شی هندسی متفاوت با یکدیگر متقارن هستند ، اگر در کنار هم، یک شکل متقارن را تشکیل دهند.

بسته به تعداد ابعاد در نظر گرفته شده، تقارن های مختلف زیر وجود دارد:

فهرست مطالب

تقارن در یک بعدی

در تک بعدی، یعنی روی یک خط مستقیم، تقارن به یک نقطه و تقارن ترجمه (جابجایی) وجود دارد.

تقارن در دو بعد

محوری تمایز قائل شد نقطه ای و در دو بعد، باید بین تقارن . علاوه بر این، تقارن های انتقالی نیز در اینجا رخ می دهد، اما اشکال دیگری از تقارن که نمی توانند در فضای یک بعدی وجود داشته باشند نیز وجود دارد.

تقارن چرخشی / تقارن چرخشی

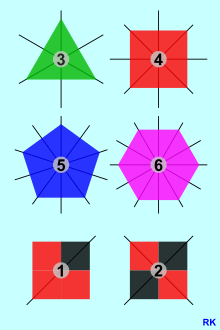
دوبعدی یک شکل هندسی دارای خاصیت دورانی متقارن بودن است که شکل دارای یک نقطه مرکزی باشد و هنگامی که در حول این نقطه بچرخد شکل به خود نقشه می‌دهد. یک دایره یا یک حلقه به معنای باریک تر به صورت چرخشی متقارن هستند. چرخش با هر زاویه ای آن را بر روی خود ترسیم می کند.

اگر بتوان آن را با چرخش در یک زاویه ثابت بر روی خود ترسیم کرد، به شکل متقارن دورانی نیز گفته می شود. فی چه 0 درجه < فی کمتر از 360 درجه حول نقطه مرکزی چرخیده است. [1] زاویه چرخش را فقط می توان با تقسیم زاویه کامل بر یک عدد طبیعی به دست آورد n > 1 بوجود می آیند، بنابراین فی = 360 ∘ n . این شماره n یک شکل کلیدی از تقارن چرخشی است و به آن “شمارش پذیری” نیز می گویند. [2] این تقارن نیز بر این اساس نامیده می شود n –شمار یا n تقارن چرخشی برابر (مشابه انگلیسی) n -تقارن چرخشی برابر”) یا همچنین ” n -تقارن چرخشی برابر”. [3]

چند ضلعی های منتظم اشکال متقارن دورانی معمولی هستند. نمودار سمت راست چهار مورد اول را نشان می‌دهد که در هر مورد بزرگ‌ترین شکل ممکن وجود دارد n از تقارن دورانی ترسیم شده است. علاوه بر این، دو شکل دیگر نشان داده شده است، یکی بدون و دیگری با تقارن چرخشی دوگانه. در مورد بی اهمیت n = 1 بی اهمیت بخواهد. هیچ تقارن چرخشی/چرخشی وجود ندارد و شاخص 1 در زمینه ریاضی استفاده نمی شود مگر اینکه گروه چرخه ای سی 1 علامت، که فقط از شکل یکسان تشکیل شده است .

نمادی نماد شناسی Schoenflies تقارن تقارن چرخشی قرار می دهد . عناصر تقارن و گروه های برای سی n محکم هستند که در زیر نشان داده شده‌اند متقارن نقطه‌ای مثال‌های بیشتر از تقارن چرخشی دو برابری شکل‌های . با این حال، این واقعیت که اجسام متقارن نقطه ای همیشه متقارن چرخشی نیز هستند، فقط در دو بعد صدق می کند.

تقارن آینه / تقارن محور

آینه ای تقارن شکلی از تقارن است که در اجسامی که بر یک محور تقارن عمود آینه شده اند رخ می دهد (نقشه سمت راست را ببینید). [4] است در دو بعد، مترادف با تقارن محوری یا تقارن محوری . برای هر محور بازتاب اعمال می شود:

1. شکل و تصویر با یکدیگر همخوانی دارند.
2. طول خط و تصویر یکسان است.
3. زاویه و زاویه دید برابر است.
4. اگر جهت چرخش در شکل تعریف شده باشد، شکل و شکل تصویر دارای جهت چرخش متفاوتی هستند.

نمونه ها

• مثلث ها می توانند یک یا سه محور تقارن آینه ای داشته باشند: مثلث متساوی الساقین متقارن محوری نسبت به عمود بر قاعده است. مثلث های متساوی الاضلاع همگن دارای سه محور تقارن آینه ای هستند که در نمودار زیر نشان داده شده است. این واقعیت که تعداد محورهای تقارن در این چند ضلعی ها به رنگ نشان داده شده با تعداد تقارن های دورانی ذکر شده در بالا مطابقت دارد، به طور کلی صدق نمی کند، زیرا بسیاری از اجسام متقارن دورانی هستند که تقارن آینه ای ندارند، برای مثال اشکال نقطه-متقارن. در ذیل نشان داده شده است.
• چهارضلعی ها می توانند یک، دو یا حتی چهار محور تقارن آینه ای داشته باشند:
  • حداقل یک محور تقارن آینه ای در ذوزنقه های متساوی الساقین (از طریق نقاط میانی اضلاع موازی) و بادبادک ها (در امتداد یک مورب) یافت می شود.
  • حداقل دو محور تقارن آینه ای در مستطیل (نصف سازها از اضلاع مخالف) و در لوزی (هر دو مورب) وجود دارد.
  • همگن در نهایت مربع مستطیل و لوزی است و چهار محور تقارن آینه ای دارد. اگر “پر” باشد، می توان تعداد را کاهش داد، همانطور که گرافیک مجاور نیز نشان می دهد.
• دایره ها و حلقه ها حتی بی نهایت محورهای تقارن دارند، زیرا در مورد هر محوری که از مرکز می گذرد متقارن هستند.
• شکل دیگری با بی‌نهایت محورهای تقارن، خط مستقیم است . از آنجایی که بی نهایت طولانی است، در مورد هر محور عمود بر آن و محوری که روی خود قرار دارد متقارن است.

تقارن محوری نمودارهای تابع

وظیفه ای که در ریاضیات مدرسه بسیار محبوب است، عبارت است از اثبات تقارن محوری برای نمودار یک تابع . این تأیید به ویژه در مورد تقارن محور y (دکارتی) سیستم مختصات آسان است . یک تابع نسبت به محور y متقارن است اگر:

f ( – ایکس ) = f ( ایکس )

اگر برای همه x معتبر باشد، تقارن محوری وجود دارد، یعنی f یک تابع زوج است .

این شرط به داشتن مقادیر تابع مخالف برای همان آرگومان ها خلاصه می شود ایکس و – ایکس باید مطابقت داشته باشند.

به طور کلی تر: نمودار تابع f فقط متقارن محور با خط معادله است. ایکس = آ ، اگر شرط زیر برای مقادیر دلخواه x صادق باشد :

f ( آ – ایکس ) = f ( آ + ایکس )

با تعویض ایکس با ایکس – آ یک شرط معادل را بدست می آورد:

f ( 2 آ – ایکس ) = f ( ایکس )

تقارن حروف بزرگ لاتین

در شکل تقارن حروف بزرگ لاتین، 26 حرف با توجه به ویژگی های تقارن هندسی به پنج گروه تقسیم می شوند. حروف FGJLPQR هیچ تقارنی ندارند. NSZ از نظر چرخشی دو برابر متقارن هستند. AMTUVWY به یک خط آینه عمودی و BCDEK به یک خط آینه افقی متقارن هستند. حروف HIOX بیشترین تقارن را با چهار عنصر تقارن نشان می دهد.

ویژگی های متقارن حروف باید به گونه ای درک شوند که لزوماً برای هر قلمی وجود نداشته باشند. برای مثال، B در بسیاری از فونت‌ها متقارن آینه‌ای نیست (مثلاً ب ، اما در شکل انتخاب شده در اینجا بسیار خوب است. به طور کلی می توان گفت که با حروف کج تمام تقارن آینه ای حروف از بین می رود، اما تقارن نقطه ای حفظ می شود.

تقارن هندسی نیز در برخی کلمات وجود دارد. است . به عنوان مثال، OHO دارای چهار عنصر تقارن است، OTTO دارای یک خط عمودی و BOB یک خط آینه افقی این کلمات نیز پالیندروم کلمات هستند . سقف و HEATH به صورت آینه ای متقارن به یک خط مستقیم افقی هستند.

تقارن نقطه

تقارن نقطه ای ، همچنین تقارن مرکزی ، [4] است هندسی یکی از ویژگی های اجسام نامیده می شود (به خودی خود) نقطه متقارن وجود داشته باشد . یک جسم هندسی (مثلاً یک چهار ضلعی) در صورتی که انعکاس نقطه ای که این جسم را روی خودش ترسیم کند . نقطه ای که این بازتاب در آن رخ می دهد مرکز تقارن نامیده می شود .

نمونه ها

• یک چهار ضلعی باشد تقارن نقطه ای (به خودی خود) دارد اگر و فقط اگر متوازی الاضلاع . مرکز تقارن در این حالت محل تلاقی قطرهای آن است. نیز به عنوان موارد خاص متوازی الاضلاع، مستطیل ، لوزی و مربع تقارن نقطه ای دارند.
• هر دایره ای (به خودی خود) نقطه متقارن با مرکز خود است.
• دو دایره با شعاع یکسان نقطه متقارن با یکدیگر هستند. مرکز تقارن نقطه وسط خط اتصال بین دو مرکز دایره است. در مورد تقارن نقطه ای، خطوط متقارن متقابل همیشه هم طول هستند.

تقارن نقطه ای نمودارهای تابع

یک کار رایج، به ویژه در ریاضیات مدرسه، اثبات این است که نمودار یک تابع معین نقطه -متقارن است. این اثبات را می توان با فرمول زیر ارائه کرد:

f ( آ + ایکس ) – ب = – f ( آ – ایکس ) + ب .

برآورده شود اگر این معادله برای تمام x ها ، تقارن نقطه ای به نقطه ( a,b ) وجود دارد. در مورد خاص تقارن نقطه در مورد مبدا (0,0)، این معادله ساده می شود:

f ( – ایکس ) = – f ( ایکس ) .

معتبر باشد اگر برای همه x ، تقارن نقطه ای نسبت به مبدأ مختصات وجود دارد.

تقارن ترجمه

ارقامی که با یک جابجایی یا ترجمه (که هویت نیست) به خود تبدیل شده اند، تقارن ترجمه ای دارند . نیز به آنها دوره ای می گویند .

• ارقامی که از نظر ترجمه متقارن هستند لزوماً باید بدون محدودیت باشند. این عملاً هرگز در کاربردهای ریاضی صدق نمی کند، به همین دلیل است که زیر مجموعه های محدود مجموعه های تناوبی ( شبکه ، ساختار بلوری ، و غیره) نیز در آنجا دوره ای نامیده می شوند.
• یک تابع f : ایکس → Y ترجمه ثابت است اگر بردار باشد آ → ∈ ایکس می دهد با f ( ایکس → ) = f ( ایکس → – آ → ) برای همه ایکس → ∈ ایکس .
• نمودارهای توابع واقعی تناوبی مانند تابع سینوس تقارن انتقالی را در یک جهت نشان می دهند.

در یک شبکه با بردارهای پایه آ → ، ب → ، ج → می تواند توسط بردار ترجمه تی → هر نقطه با مقادیر صحیح از تو ، v ، w برسد. زاویه بین آ → ، ب → ، ج → خودسرانه است بردارهای پایه نیز بردارهای ترجمه هستند و با هم سلول واحد را در بر می گیرند . [5]

تی → = تو ∗ آ → + v ∗ ب → + w ∗ ج →

تقارن مقیاس

در برخی زمینه های ریاضی و فیزیکی، تغییرناپذیری یک شی در هنگام بزرگ شدن یا کوچک شدن به عنوان تقارن مقیاس یا عدم تغییر مقیاس نامیده می شود . این پدیده با به اصطلاح فراکتال ها بسیار واضح می شود .

تقارن تعویض رنگ

یکی دیگر از تقارن هندسی، تقارن تعویض رنگ است. می توانید چرخش ها و بازتاب ها را با تعویض رنگ ترکیب کنید. همانطور که قبلاً گفته شد، دو شکل مختلف می توانند با یکدیگر متقارن باشند. تقارن در این مورد رابطه دو جسم است. این در مورد تقارن تبادل رنگ نیز صدق می کند. از سوی دیگر، اگر یک شکل دارای تقارن های مبادله رنگ باشد، در این صورت متقارن با تعویض خودکار رنگ است. متقارن تعویض خودکار رنگ، شکلی است که پس از چرخش و/یا آینه سازی و سپس تعویض رنگ ها (یا برعکس) مانند قبل به نظر می رسد. [6]

نمودار “نمونه هایی از جفت های متقارن رنگ” دو شکل متقارن رنگ را نشان می دهد. تقارن های “کلاسیک”، تعدد و خطوط تقارن آینه ای، در صورت وجود به شکل ها کشیده می شوند. نوع و تعداد تقارن ها در یک جفت شکل متقارن مبادله کننده رنگ یکسان است. فقط جفت پایین نمودار چنین تقارن هایی ندارد. متقارن تعویض خودکار رنگ یکی از این ارقام نیست. دو چهره یک زوج نباید به عنوان “مثبت” و “منفی” توصیف شوند، زیرا این اصطلاحات در عکس استفاده می شوند . نیز ربطی به رنگ های مکمل تعویض رنگ ندارد.

در مورد ساده یک فیگور دو رنگ، و ما می خواهیم در اینجا خود را به این محدود کنیم، دو پیش شرط وجود دارد که اصلاً متقارن بودن آن با تبادل خودکار رنگ باشد. اگر رنگ ها را حذف کنید، شکل خطوط باید متقارن باشد. از طرف دیگر، قسمت های جزئی که رنگ های متفاوتی به خود می گیرند باید همخوان باشند و در نتیجه دارای مساحت یکسانی باشند.

نمودار «نمونه‌هایی از شکل‌های متقارن متقارن کلاسیک و تعویض خودکار رنگ‌ها» سه ستون از 7 شکل را نشان می‌دهد که وقتی چهار مربع از مربع کوچک بالا به هم متصل می‌شوند تا مربع بزرگ‌تری را تشکیل دهند و به‌طور خاص در این فرآیند چرخانده شوند، ایجاد می‌شوند. این در مورد شکل های نمودار اول نیز صدق می کند. برای هر شکل، عناصر تقارن آن، تعدد در مورد تقارن دورانی و خطوط تقارن آینه‌ای ترسیم می‌شوند.

ستون اول و دوم خطوط رنگی یا نواحی رنگی و تقارن “کلاسیک” آنها را نشان می دهد. کثرت با 4 یا 2 سیاه مشخص شده است، خطوط تقارن آینه آبی هستند. دو شکل پایین و شکل ششم (از پایین شمارش شده) ستون مرکزی تقارن “کلاسیک” ندارند، اما دارای تقارن های تغییر رنگ هستند.

تقارن های تبادل رنگ در شکل های ستون سوم ترسیم شده است. هر عمل تقارن از دو عمل ناشی می شود، چرخش یا آینه سازی و در عین حال از تبادل رنگ ها. تعدد با 4 یا 2 سفید مشخص شده است، خطوط تقارن آینه تبادل رنگ سبز هستند. همانطور که می بینید، تقارن شکل های طرح کلی به تقارن “کلاسیک” و تقارن تغییر رنگ تقسیم می شود.

تقارن در سه بعدی

در طبیعت

فیزیک – اکثریت قریب به اتفاق گونه های جانوری و ساختار بسیاری از اندام های گیاهی از بیرون تقریباً آینه ای متقارن است – که در زیست شناسی به آن متقارن دو طرفه می گویند با یک نیمه چپ و راست. تنها صفحه تقارن (تک تقارن) صفحه میانه تشریحی است . اچ. صفحه ساژیتال میانه (مرکزی)؛ این هر صفحه ای از بدن است که از جلو به عقب و از بالا به پایین امتداد دارد. 95 درصد از همه گونه های جانوری، از جمله انسان، بیلتریا (“حیوانات دو طرفه”) با تقارن بدنی همنام هستند (دیگر حیوانات بسیار اصلی (مانند چتر دریایی ) اغلب با توجه به یک محور طولی تقارن چرخشی دارند، بدن آنها بنابراین یک بدنه تقریبی از انقلاب ). می توان با توجه به تک تقارن دو طرفه، سطوح و جهت های واضح بدن را تعریف کرد که توصیف تشریحی را ساده می کند. با این حال، تقارن بدن کامل نیست، بنابراین تعداد زیادی مجرد (جفت نشده) اندام های داخلی (مانند قلب) از تقارن آینه ای حذف می شوند. تمام اجزای بدن که به طور متقارن طراحی شده اند، مانند چشم ، گوش ، بازو ، پا ، سینه و غیره انسان نیز دارای انحرافات جزئی در موقعیت، شکل و اندازه از یکدیگر هستند.

در جانورشناسی، در بیلتریا که تقارن شعاعی پنج پرتوی خارپوستان، منحصر به فرد است، به عنوان پنتامریسم شناخته می شود (یعنی در ستاره دریایی پنج صفحه تقارن از محور چرخش مرکزی عبور می کنند). در ریاضیات، ویژگی های تقارن ستاره دریایی را می توان با یک گروه چرخشی توصیف کرد . ( لارو ستاره‌های دریایی مانند بسیاری از حیوانات دیگر این گروه هنوز به صورت دو طرفه متقارن هستند. در طول دگردیسی پنتامری فقط ایجاد می‌شود.)

بدون تقارن، i. اچ. نامتقارن ، بدون بافت هستند ( اسفنج و پلاکوزوآ ).

معادل عناصر تقارن دو بعدی

تقارن محوری در دو بعدی با تقارن آینه ای نسبت به صفحه در سه بعدی مطابقت دارد. تقارن نقطه ای در دو بعدی با تقارن محوری (تقارن چرخشی 180 درجه) مطابقت دارد. وجود دارد علاوه بر این، تقارن نقطه/مرکز در فضا و مانند صفحه، تقارن انتقالی .

تقارن چرخشی / تقارن چرخشی / تقارن استوانه ای

اجسام سه بعدی از نظر چرخشی متقارن هستند اگر محوری وجود داشته باشد که چرخش در زوایای دلخواه جسم را بر روی خود ترسیم کند. تقارن چرخشی که به این شکل تعریف می شود، تقارن استوانه ای نامیده می شود . محور یک محور تقارن جسم نسبت به چرخش است. اجسام هندسی سه بعدی با این خاصیت اجسام انقلاب نامیده می شوند .

مشابه دوبعدی، مفهوم تقارن چرخشی یا چرخشی نیز زمانی استفاده می‌شود که بتوان جسم را با چرخش در یک زاویه خاص حول یک محور بر روی خود ترسیم کرد. به عنوان نمونه هایی از اجسام سه بعدی متقارن دورانی، گرافیک مجاور منشورهایی را به صورت پرسپکتیو نشان می دهد که زمانی ایجاد می شوند که چند ضلعی های دوبعدی در نمودار بالا، چهار چند ضلعی منظم و دو شکل هندسی دیگر را با شکل های کلیدی تقارن چرخشی خود در امتداد یک خط مستقیم عمود بر شکل حرکت دهند. در فضا تبدیل شود. نیز یاد می شود از این روش به عنوان اکستروژن چند ضلعی خاص . منشورهای مستقیم به وجود می آیند، چندوجهی های ، که در این مورد، وقتی چند ضلعی های داده شده چند ضلعی های منتظم هستند، منشورهای منظم نامیده می شوند.

مرکز تقارن یک جسم دوبعدی، از طریق اکستروژن، به محور چرخش با سر پیکانی تبدیل می‌شود که می‌توان از آن برای تعیین اینکه آیا زاویه چرخش باید مثبت یا منفی شمرده شود، استفاده کرد . تقارن های نشان داده شده متعلق به گروه های حلقوی هستند سی 1 بیس سی 6 و زیرگروه هایی از گروه های تقارن کامل مربوط به منشورها هستند. لازم به ذکر است که این اجسام سه بعدی دارای تقارن چرخشی و آینه ای اضافی هستند. تقارن های دورانی یک مکعب همگن به عنوان نماینده شش منشور منظم نشان داده شده در نظر گرفته شده است در بخش زیر، تمام .

تقارن چرخشی یک مکعب

یک مکعب همگن در مجموع دارای 13 محور چرخش (محورهای تقارن چرخشی) است که در نمودار زیر نشان داده شده است:

• 3 از طریق مراکز چهره های مخالف،
• 4 از طریق گوشه های مخالف و
• 6 عبور از وسط لبه های مخالف.

اگر عناصر تقارن تقارن چرخشی مکعب را بشماریم عبارتند از: عنصر خنثی ، هر کدام 3 عدد برای 4 برابر، 2 عدد برای 3 برابر و هر کدام یکی برای محورهای چرخش 2 برابر. اینها در کل هستند 1 + 3 ⋅ 3 + 4 ⋅ 2 + 6 ⋅ 1 = 24 عناصر تقارن

تشکیل می دهند این 24 عنصر با هم گروه چرخان تاس را . مکعب و هشت وجهی منظم جامدات هستند دوتایی افلاطونی و تقارن یکسانی دارند. بنابراین، گروه چرخش مکعب و گروه چرخش هشت وجهی با هم در مقاله گروه هشت وجهی مورد بحث قرار گرفته اند . اگر گروه چرخش مکعب را با بازتاب نقطه ای در مرکز مکعب ترکیب کنیم، نتیجه می شود 2 ⋅ 24 = 48 عناصر گروه تقارن کامل مکعب ( به زیر مراجعه کنید ).

تقارن آینه ای

تقارن آینه ای به دو معنا به کار می رود:

• اگر صفحه ای وجود داشته باشد جسمی دارای تقارن آینه ای است و انعکاس آن صفحه یک عمل تقارن بدن مورد بررسی است. پس از انعکاس، جسم مشاهده شده با خودش همخوانی دارد. صفحه تقارن آینه شناخته می شود نیز به سادگی به عنوان صفحه آینه [7] . به این معنا، تقارن آینه ای یک اتومورفیسم است . در ریاضیات، بر روی خود را اتومورفیسم نگاشت یک شی ریاضی می نامند که در آن شی و شی نگاشت شده قابل تشخیص نیستند. [۸]

• دو گفته می شود که جسم با یکدیگر متقارن آینه ای هستند اگر فقط با انعکاس در یک صفحه متفاوت باشند. در زبان محاوره ای از یک کپی معکوس آینه ای (یا یک تصویر وارونه آینه ای ) صحبت می شود. موقعیت دو جسم در فضا مهم نیست. بنابراین ممکن است ابتدا یک ترجمه و یک چرخش قبل از یافتن یک صفحه آینه مشترک لازم باشد. دو کلیسای سانتا ماریا دی مونته سانتو و سانتا ماریا دی میراکولی در پیازا دل پوپولو در رم (تقریباً) آینه‌ای متقارن و روبه‌رو هستند، به طوری که احتمالاً آینه‌کاری بدون جابجایی امکان‌پذیر است. در این صورت، کلیساها نیز متقارن آینه ای در اولین معنای اصطلاحی که در بالا توضیح داده شد، خواهند بود. یکی دیگر از نمونه‌های کلاسیک دو ساختمان متقارن آینه‌ای، ساختمان‌های دادگاه پادشاه چارلز و دادگاه ملکه آن در توسط کریستوفر رن ساخته شده است . کالج سلطنتی نیروی دریایی، است که گرینویچ .

اجسام بسیار متقارن (مانند برخی از منشورهای نمودار زیر) می توانند صفحات آینه ای زیادی داشته باشند که همگی در یک نقطه قطع می شوند. یک کره دارای تعداد بی نهایت صفحه آینه است. در نمودار زیر در سمت راست، چهار صفحه از 9 صفحه آینه و یکی از 13 محور چرخش یک مکعب همگن نشان داده شده است. صفحات آینه در محور چرخش 4 برابر یکدیگر را قطع می کنند. تقارن نشان داده شده از نوع گروه دو وجهی است D 4 و زیرگروهی از گروه مکعب است . 48 عنصر تقارن گروه مکعب در مجموع مکعب را به 48 حوزه اساسی (معادل) تقسیم می کنند .

تقارن آینه دوار

تقارن آینه دوار تقارن جسمی است که از دو عملیات فرعی تشکیل شده است. اولین عملیات فرعی چرخش حول محور، محور آینه دوار، دومی بازتاب در صفحه عمود بر محور دوار، صفحه آینه دوار است. [9] این صفحه از مرکز تقارن، از مرکز بدن عبور می کند. اگر صفحه آینه دوار صفحه تقارن آینه ای بدنه نباشد، هر دو عملیات جزئی به صورت جداگانه عملیات تقارن نیستند، بلکه فقط ترکیب آنها هستند. ترتیب عملیات فرعی مهم نیست. همچنین می توانیم ابتدا آینه سازی و سپس چرخش را انجام دهیم.

تقارن آینه دوار یک مکعب

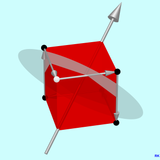
انعکاس چرخشی اجسام بر روی خود یکی از کمتر شناخته شده اما شاید جالب ترین عملیات تقارن است که به راحتی با استفاده از گرافیک مناسب قابل درک است. سه تصویر یک مکعب و هر یک از محورهای آینه دوار و صفحات آینه چرخان مرتبط با آنها را نشان می دهد. به منظور تمایز صفحات آینه دوار از صفحات تقارن آینه ای، آنها به صورت دیسک های دایره ای خاکستری نشان داده می شوند که به صورت تصویری به صورت بیضی ظاهر می شوند. برای مکعب های گرافیک انتخاب شد حالت ترسیم نیمه شفاف . از آنجایی که محورهای آینه دوار نیز محورهای چرخش هستند، آنها به ترتیب تمام 13 محور تقارن دورانی مرتب شده اند… گرافیک بالا .

اولین تصویر از سه گرافیک یکی از سه محور آینه چرخان 4 برابری و صفحه آینه چرخان مرتبط را نشان می دهد. اثر بازتاب چرخشی را می توان با دنبال کردن مسیر گوشه ای که با یک نقطه سفید مشخص شده است درک کرد. صفحه آینه دوار از طریق محور آینه دوار جهت گیری می کند. بنابراین می توان گفت که نقطه سفید بالای صفحه آینه در حال چرخش قرار دارد. پس از چرخش 90 درجه (قانون دست راست: شست در جهت محور، چرخش در جهت انگشتان دیگر)، ابتدا نقطه به گوشه بالا سمت راست و از طریق بازتاب به گوشه پایین سمت راست ترسیم می شود. که با یک نقطه سیاه مشخص شده است. نقطه و پیکسل با یک فلش به هم متصل می شوند. آینه چرخشی مجدد به میزان 90 درجه به نقطه سیاه بالای سمت راست و غیره منتهی می شود. پس از چرخش چهار برابر آینه به نقطه شروع دوباره می رسد.

مدار یک نقطه از مکعب در موقعیت کلی یک مسیر زیگزاگی بسته فضایی در اطراف صفحه آینه در حال چرخش است. اگر نقطه ای که دنبال می کنیم روی صفحه آینه دوار باشد، مسیر آن یک مربع است. اگر روی محور آینه گردان باشد، چهار بار روی محور آینه چرخان به جلو و عقب می پرد که توسط صفحه آینه چرخان منعکس می شود. مرکز تقارن، مرکز ثقل مکعب، همیشه روی خودش نگاشت می شود. توجه داشته باشید که صفحه آینه دوار در این مورد نیز صفحه تقارن آینه ای مکعب است.

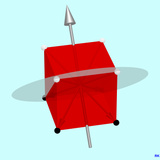
مورد نشان داده شده در نمودار دوم یکی از چهار محور آینه گردان 6 برابری است. از یک طرف جالب است زیرا صفحه آینه دوار واضح است که صفحه تقارن آینه ای مکعب نیست. از طرفی چون محور چرخش 3 برابری به یک محور آینه گردان 6 برابری تبدیل می شود. اگر مسیری را دنبال کنید که یک نقطه از مکعب دنبال می کند، می توانید ببینید که 6 برابر است، برای مثال مسیر گوشه که با یک نقطه سفید در نمودار مشخص شده است. اولین عملیات فرعی، چرخش 60 درجه حول محور آینه دوار، نقطه سفید را به نقطه ای که یک نقطه گوشه نیست، ترسیم می کند. دومین عملیات جزئی، بازتاب در سطح آینه چرخان، به اولین نقطه تصویر منتهی می شود که به عنوان یک نقطه سیاه مشخص شده و بالای سطح آینه چرخان قرار دارد (نقطه سیاه در بالا سمت راست). دوباره نقطه و پیکسل با یک فلش به هم متصل می شوند. اگر اکنون چرخش 60 درجه را دوباره روی پیکسل اول اعمال کنید، به پیکسل سیاه دوم در پایین سمت راست و غیره منتهی می شود. پس از 6 چرخش 60 درجه، دوباره به نقطه شروع سفید می رسد. اگر نقطه ای که دنبال می کنیم روی صفحه آینه چرخان باشد، مسیر حرکت آن روشن است شش ضلعی منظم .

احتمالاً تأثیر آینه‌کاری چرخشی دو برابری، که گرافیک سوم به آن اختصاص دارد، غیرمنتظره است. یکی از محورهای آینه دوار دو برابر نشان داده شده است که بر اساس قیاس محورهای چرخش، شش مورد از آن را انتظار داریم. اگر آینه‌کاری چرخشی ۲ برابری را طبق رویه‌ای که در بالا ذکر شد انجام دهیم، متوجه می‌شویم که هر نقطه از مکعب بر روی « پادپای » خود، یعنی روی نقطه‌ای که در طرف مقابل مکعب قرار دارد، نگاشت می‌شود. نقطه و نقطه تصویر با مرکز تقارن روی یک خط مستقیم قرار دارند و از مرکز تقارن یکسان فاصله دارند. در این حالت چهار نقطه سفید در گرافیک و پیکسل آنها چهار نقطه سیاه مشخص می شود. هر چهار بردار اتصال بین نقطه و نقطه تصویر در مرکز تقارن همدیگر را قطع می کنند.

همچنین جالب این واقعیت است که انعکاس‌های دوار حول هر شش محور آینه‌ای دو برابری ممکن به همان نوع تقارن منجر می‌شود. این نوع تقارن، انعکاس نقطه ای در مرکز تقارن، در نظریه گروه و کریستالوگرافی وارونگی نامیده می شود . [10] بنابراین می‌توان تمام محورهای دوار آینه‌ای دو برابر را در ملاحظات تقارن حذف کرد و آنها را با یک عملیات واحد، یعنی وارونگی، جایگزین کرد. [11]

یک انعکاس چرخشی هیچ نقطه ای از مکعب، یعنی هیچ گوشه ای، بلکه هیچ صورت یا لبه ای را در جای اصلی خود باقی نمی گذارد. تنها نقطه ثابت بازتاب چرخشی، مرکز تقارن، مرکز مکعب است که قبلاً به آن اشاره شد.

منظم و یک چهار ضلعی همانطور که نمودار با استفاده از یک محور به عنوان مثال نشان می دهد، همگن دارای تقارن آینه ای چرخشی 4 برابری یک مکعب همگن است. همانطور که از نمودار مشاهده می شود، بر خلاف مکعب، صفحه آینه دوار یک صفحه تقارن آینه ای چهار وجهی نیست. یک مدل قاب سیمی از یک مکعب محصور نیز در نمودار ترسیم شده است.

تفاوت بین آینه کاری چرخشی و چرخش

خواص بازتاب های چرخشی با خواص چرخش ها متفاوت است:

• محورهای چرخشی یک جسم نیز می توانند محورهای آینه ای دوار بدن باشند، اما هر محور چرخشی لزوماً یک محور آینه ای دوار نیست. برای مثال، با چهار وجهی، محورهای چرخش 3 برابری آن، محورهای آینه ای دوار نیستند.
• حاصلضرب عمل تقارن یک چرخش با خودش همیشه یک عنصر تقارن جدید گروه است. برای یک محور چرخش n برابر، توان تا (n-1) بالا می رود. حاصلضرب عمل تقارن یک محور آینه دوار با خودش یک عنصر تقارن جدید از گروه نیست، بلکه یک چرخش (تک) به دلیل بازتاب دوگانه است.
• تعداد یک محور چرخش و یک محور آینه دوار که در یک جهت تراز شده اند می تواند یکسان باشد (هر دو در تصویر اول مکعب 4 برابر هستند) یا می توانند متفاوت باشند (3 برابر در مورد تقارن چرخشی و 6 برابر). در صورت تقارن آینه دوار در نمودار دوم، تا کنید).
• هر محور آینه دوار یک مکعب بدون در نظر گرفتن تعداد آنها، دو عنصر تقارن در هر محور آینه دوار دارد. از آنجایی که مکعب دارای سه محور آینه گردان 4 برابری و چهار محور آینه 3 برابری است، 2 ⋅ ( 3 + 4 ) = 14 عناصر آینه ای دوار گروه مکعب به معنای باریک تر. انعکاس نقطه ای از تمام محورهای آینه چرخان 2 برابر وجود دارد علاوه بر این، یک ، وارونگی، که در مجموع 15 عنصر آینه چرخان ایجاد می کند.

همانطور که در ابتدا ذکر شد، انعکاس نقطه در جهان دو بعدی معادل یک چرخش 180 درجه به دور نقطه ثابت است و بنابراین عنصر جدایی از تقارن نیست.

تقارن نقطه / تقارن وارونگی

است همانطور که در بخش قبل توضیح داده شد، تقارن نقطه یا تقارن وارونه ، تقارن یک جسم نسبت به یک نقطه، مرکز تقارن . هر نقطه با نقطه ای که روی خط مستقیم قرار دارد که از آن نقطه از مرکز می گذرد و در سمت دیگر مرکز فاصله دارد، موقعیت خود را مبادله می کند. . انعکاس نقطه‌ای جسم روی خودش است. انعکاس نقطه‌ای هیچ نقطه‌ای از بدن را در جای اصلی خود باقی نمی‌گذارد، به استثنای یک استثنا: تنها نقطه ثابت یک بازتاب چرخشی، مرکز تقارن، مرکز بدن است

این گرافیک نقشه برداری از چهار گوشه انتخاب شده (نقاط سفید) یک مکعب را با وارونگی (نقاط سیاه) نشان می دهد. برعکس، تمام نقاط سیاه بر روی نقاط سفید نگاشت می شوند. گرافیک تکراری از گرافیک سوم بالا ( محورهای آینه چرخان انتخاب شده … ) بدون محور آینه چرخشی 2 برابر و صفحه آینه چرخان است.

جامدات افلاطونی همگن مکعب ، هشت ضلعی ، دوازده وجهی و ایکو وجهی متقارن نقطه ای هستند. ساده ترین جامد افلاطونی، از سوی دیگر، چهار وجهی منظم ، نیست.

در مورد مکعب (از جمله وارونگی) 15 تقارن آینه چرخان وجود داشت. همراه با 9 صفحه آینه، 24 عنصر تقارن به دست می‌آید، یعنی دقیقاً به تعداد عناصر گروه چرخش مکعب. این تصادفی نیست، زیرا هر آینه یا عنصر آینه دوار را می توان به عنوان ترکیبی از یک چرخش و یک وارونگی تفسیر کرد. به این معنا، وارونگی یک جسم متقارن وارونگی دارای موقعیت برجسته ای شبیه به عنصر خنثی در یک گروه تقارن است.

تقارن کروی

تقارن دورانی حول هر محوری که از همان نقطه عبور می کند مورد خاصی از تقارن دورانی است و به آن تقارن کروی یا تقارن شعاعی می گویند. ستاره ها هستند به عنوان مثال ب. تقریباً کروی متقارن است، زیرا خواص آنها (مانند. B. چگالی) در همه جا یکسان نیست، بلکه فقط به فاصله تا مرکز بستگی دارد. میدان گرانشی آنها و z. ب) میدان الکتریکی یک کره دارای بار متقارن چرخشی به صورت کروی متقارن است.